Funkcja aktywacji

Funkcja aktywacji jest jednym z kluczowych zagadnień sieci neuronowych gdyż jej odpowiedni dobór ma wielkie znaczenie dla wybranego modelu i procesu uczenia. Odpowiednie jej dostosowanie dla warstwy przyczynia się do szybkości jak i sprawności działania całej sieci. Mam nadzieję że zebrane informacje pozwolą wyjaśnić przynajmniej część problemów związanych z tym zagadnieniem. Funkcja ta decyduje o tym co zostanie przepuszczone do następnego poziomu.

Czym jest funkcja aktywacji ?

Funkcja aktywacji (mówiąc w uproszczeniu) pomaga sieci w uczeniu się skomplikowanych wzorców w danych wejściowych. Określa ona, jakie sygnały powinny zostać wysłane do następnego neuronu. W poprzednim artykule określiłem jej pozycje na przykładzie pojedynczego neuronu. Ma ona jednak zastosowanie w sieciach wielowarstwowych.

Do najpopularniejszych funkcji aktywacji należą:

Sigmoid

Sigmoid jest jedną z najczęściej używanych funkcji aktywacji, chociaż odchodzi powoli w zapomnienie. Jest to nieliniowa logarytmiczna funkcja która jest dość kosztowna obliczeniowo więc stosuje się ją dość rzadko.

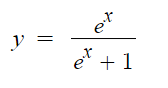
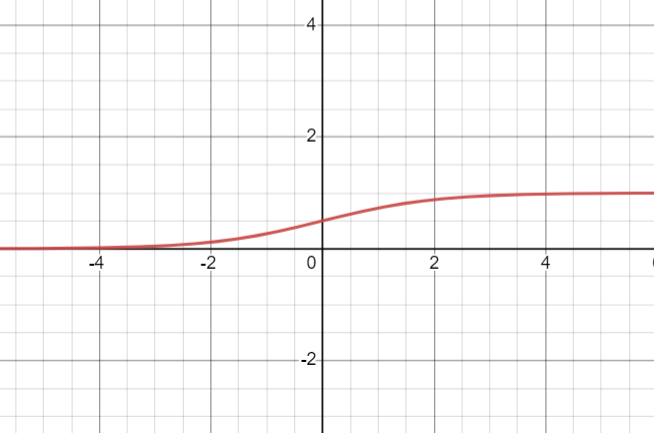
Jej wynik zawsze mieści się w przedziale od 0 do 1. Sprawia ona również różne problemy. Jednym z nich jest fakt, iż umożliwia ona nasycenie wyjścia każdego neuronu. Wszystkie wartości które są większe niż jeden będą odcinane do tej wartości. Analogicznie przedstawia się sytuacja dla wartości mieszczących się poniżej zera. Wokół punktu środkowego czułość funkcji sigmoidalnej jest natomiast najwyższa (0, 0,5). Funkcja ta jest zatem szczególnie przydatna przy problemach z klasyfikacją binarną.

Tanh

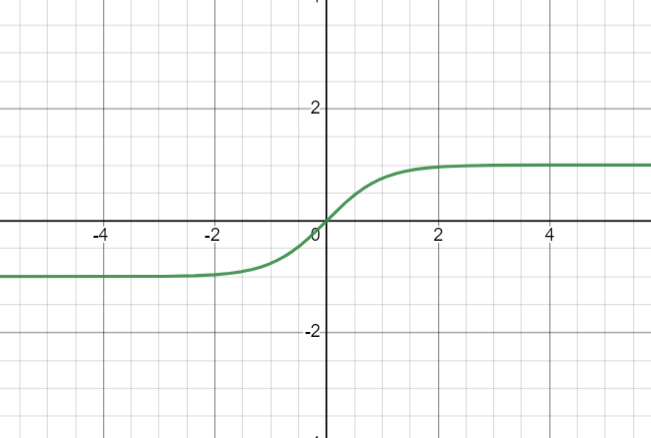
Funkcja hiperboliczna (tanh) jest bardzo podobna do funkcji sigmoidalnej. Tanh jest symetryczny w punkcie zero, a wartości mieszczą się w zakresie od -1 do 1.

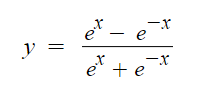
Tak jak w przypadku sigmoidu jest ona bardzo czuła w punkcie centralnym (0, 0), ale nasyca się dla bardzo dużej liczby (dodatniej i ujemnej). Ta symetria czyni ją lepszą niż funkcja sigmoidalna lecz nadal jest ona obliczeniowo kosztowna. Gradient jest silniejszy niż w przypadku sigmoid (pochodne są bardziej strome), ale podobnie jak sigmoid, tanh ma również problem znikającego gradientu i nasycenia.

ReLU (Rectified Linear Unit)

Z powodu jej niebywałych zalet jest to obecnie najbardziej rozpowszechniona i szeroko używana funkcja aktywacji.

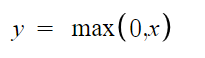
Jak widać jej obliczenie jest bardzo proste. Dodatkowo nie ma ona problemu wynikającego ze znikającego gradientu oraz nasycenia. Taka nieliniowość pozwala na zachowanie i uczenie wzorów znajdujących się wewnątrz danych. Część liniowa zaś sprawia że dane są łatwiejsze do interpretacji. Czyżby funkcja idealna? Otóż nie do końca. Jej problemem jest nie wyśrodkowanie względem zera co może powodować kolejne problemy. Jej kształt powoduje problem nazywany “umierajacym ReLU” (dying ReLU). Oznacza to iż niektóre węzły całkowicie “umierają” nie ucząc się niczego ponieważ dla wszystkich ujemnych wartości wejściowych ich wyjście będzie wynosiło zero. Kolejny problem z ReLU to niekontrolowany przyrost wartości ( aż do nieskończoności ) co może prowadzić do tworzenia kolejnych bezużytecznych węzłów. Dzięki swoim właściwościom idealnie nadaje się do sieci konwolucyjnych (CNN). Nie nadaje się jednak do sieci rekurencyjnych (RNN, LSTM, GRU).

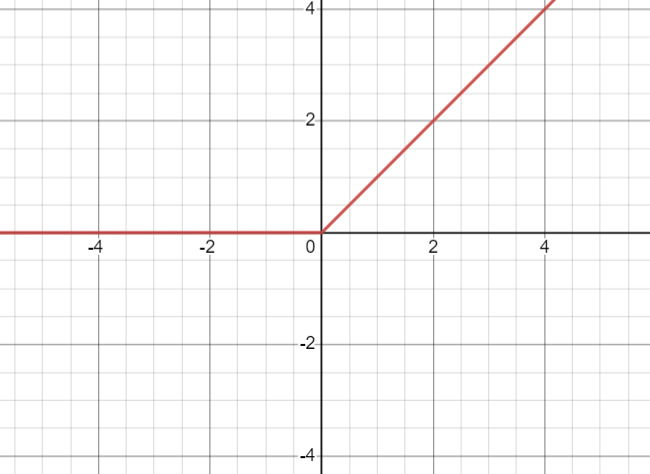
Leaky ReLU

Jest to modyfikacja funkcji ReLU która miała naprawić jej wadę związaną z obumieraniem neuronów.

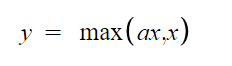
Jak widać wprowadzono dodatkowy parametr który zmniejsza możliwość odcinania wartości mieszczących się poniżej zera. Najczęściej wartość tego parametru ustawiona jest w okolicy 0.01. Można również zauważyć iż jeśli ustawimy parametr na wartość równą jeden otrzymamy zwykłą funkcję liniową. Dlatego parametr ten nigdy nie zbliża się do tej wartości.

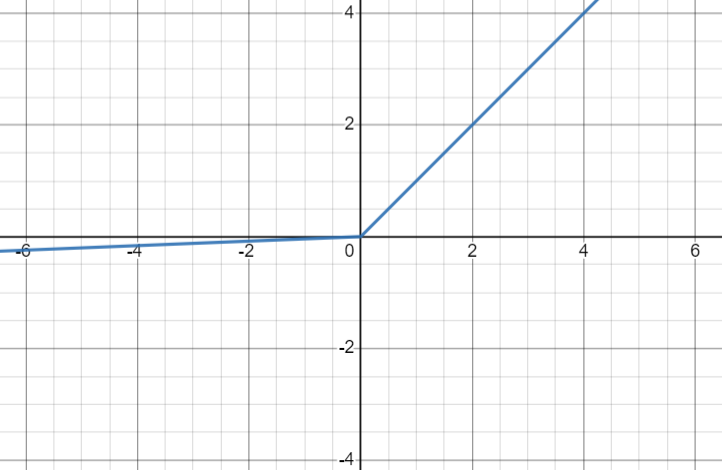
ReLU 6

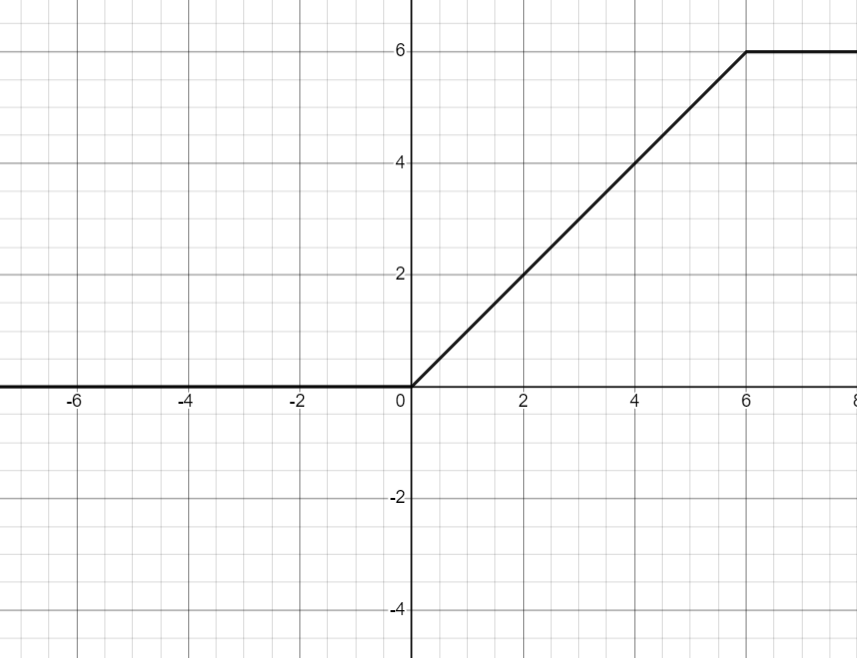
Jest to kolejna modyfikacja funkcji Realu która naprawia kolejną jej wadę jaką jest niekontrolowany przyrost wartości.

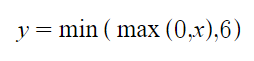
Jak widać odcięcie następuje dopiero po szóstce. Jest to dość duża wartość która w wielu przypadkach jest wystarczająca.

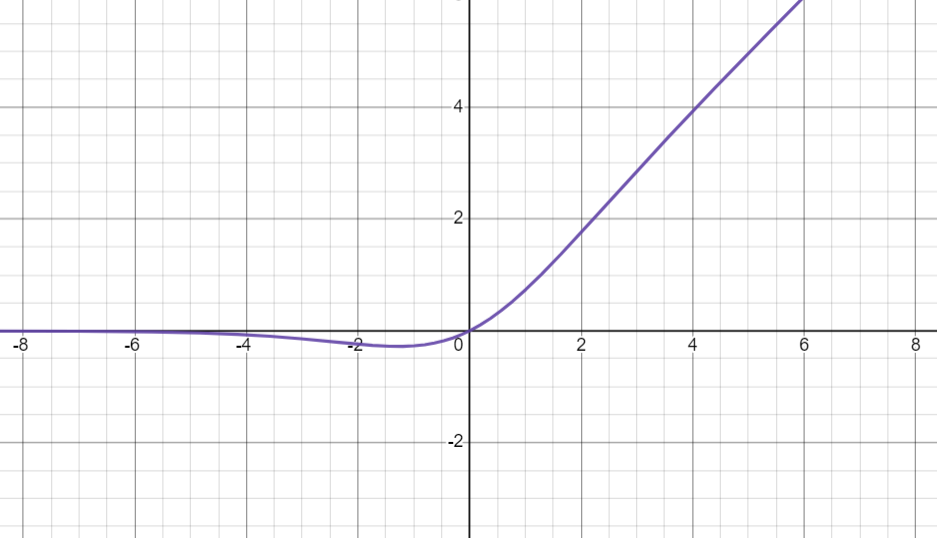
Swish

Funkcja ta jest wariantem funkcji sigmoidalnej. Należy ona do jednych z najnowszych.

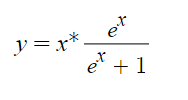
W 2017 roku badacze Google doszli do niej podczas prac nad ImageNet. Wykazali oni iż wykorzystanie tej funkcji poprawia wydajność w porównaniu do funkcji ReLU i sigmoid.

Jak dobierać funkcje aktywacji?

Jak wspomniałem wcześniej funkcja sigmoidalna oraz Tanh powodują problemy ze zanikającym gradientem. Powinny więc być używane z rozwagą (choć czasem nie ma innego wyjścia).

cdn...